这个章节我们要学习7种重要的的分布--the uniform, binomial, normal , lognormal , student's t, chi-square, F-distribution

1) 离散随机变量。如骰子

2)凡事连续的随机变量，不管能不能取到这个值，它的概率都是0， P(x)=0  even though x can occur. 正因为如此，我们只能退而求其次，取该值附近的值的概率。也称为概率密度函数pdf， 举例， 正态分布是连续的随机变量，所以，有没有等于好，面积一样，寄概率一样。

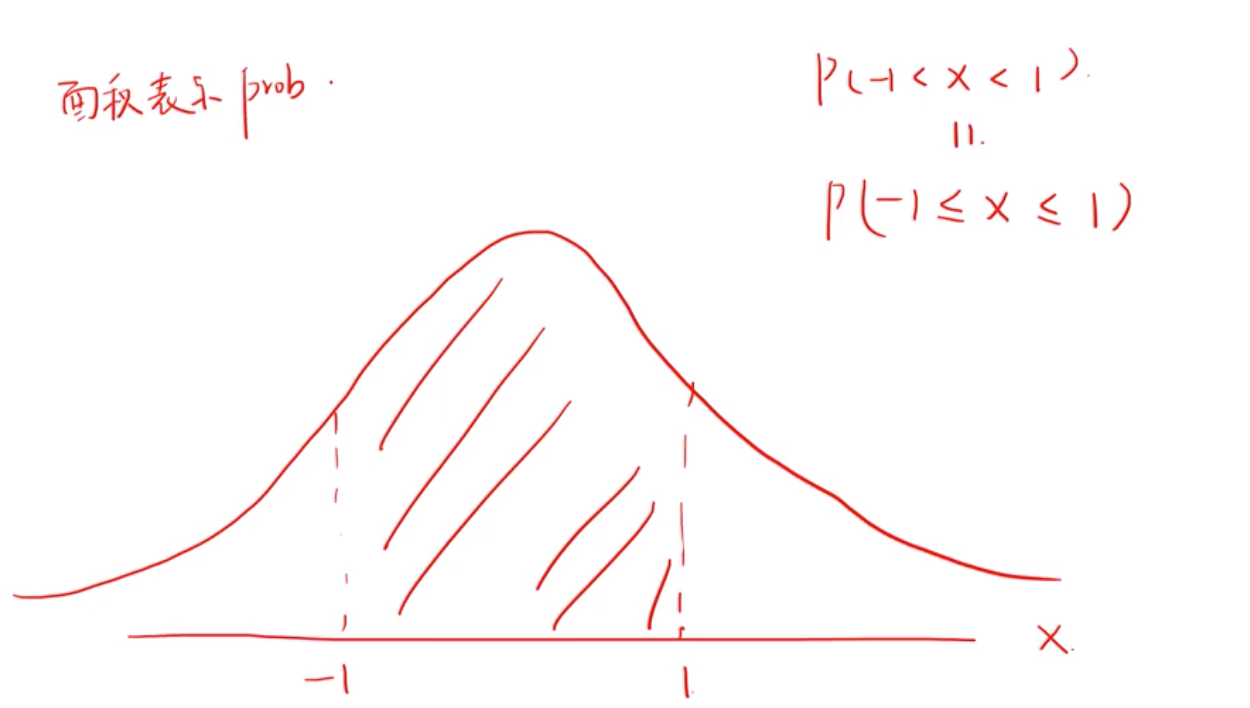
第一种，离散均匀分布，discrete uniform distribution

第二种，二项离散分布

可分为 Bernoulli 伯努利分布 （bernoulli distribution ）和二项随机分布（binomial distribution）

注意： 伯努利分布是只做一次实验的二项随机分布，二项随机分布是多次的伯努利随机分布

伯努利的条件是1） 独立事件 2） 概率稳定

要如何求bernoulli random variable 的期望和方差呢？

求ernoulli random variable 的期望（expectation-均值）E(x)=1*p +0*(1-p)=p 

求variance =方差就是点到均值的距离的平方的平值（有权重=概率）

故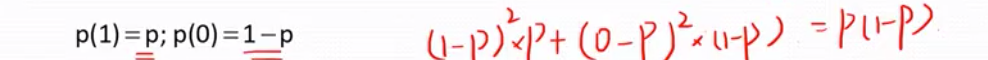

明白了伯努利随机变量的期望和方差就可以继续拓展，二项随机变量就是多次的伯努利事件，所以分别✖️n 次就是二项随机变量的期望和方差