第三种： 连续均匀分布

1） 在某一个区间内去到某值的概率为0 

2）正态分布 normal distribution

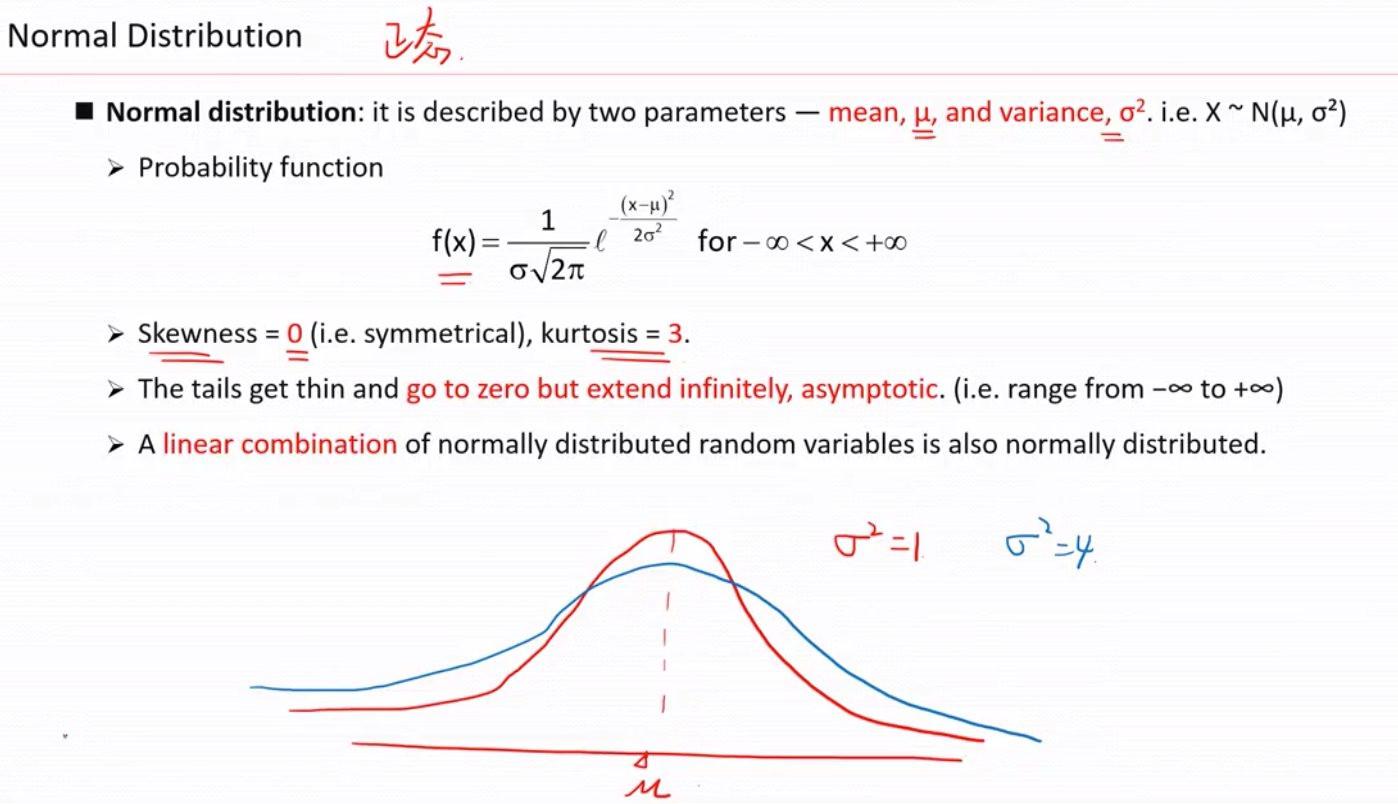
正态分布的3个性质

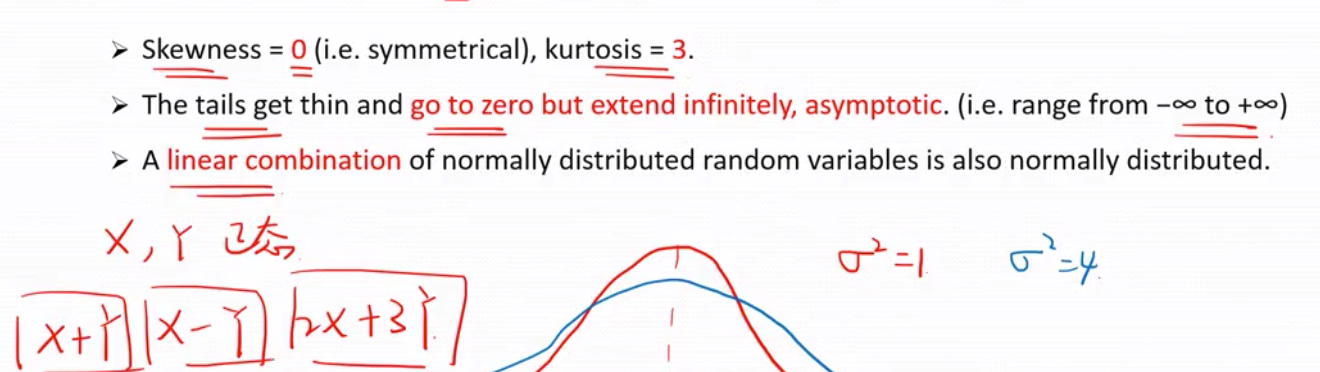
1）偏度为 0 ，峰度为3

2）长尾无限趋近于0单不等于0 ， 即范围是负无穷到正无穷

3）服从正态分布的几个随机变量的线性表达式也符合正态分布

置信区间--对于服从正态分布，反映的是落在1倍，1.65倍，1.96倍，2.58倍标准差的区间的概率 68%，90%，95%，99% （常用这几个）

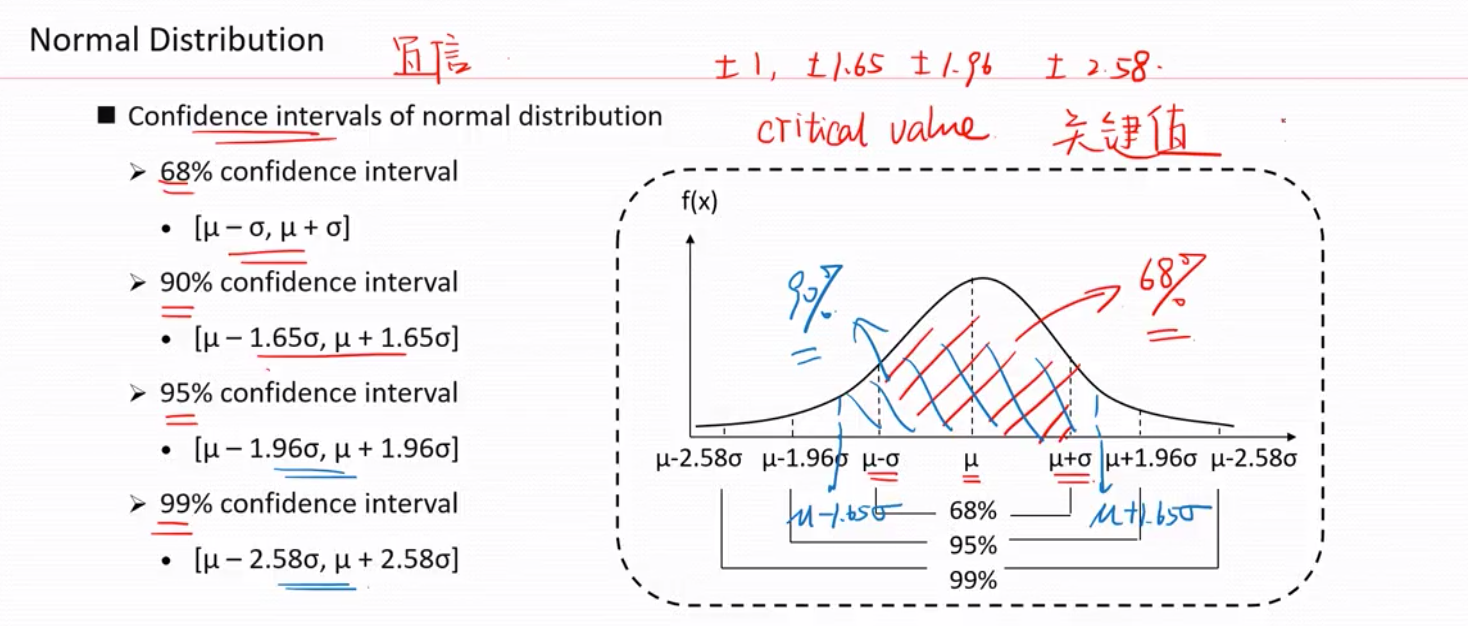
正态分布标准化后得到标准正态分布，通常用z 表示，故又称 z 分布

1，1.65，1.96， 2.58 是置信区间的关键值（临界值）常用要背。

第四种： 对数正态分布 log normal distribution

对数正态分布的性质

1） 取值必须>0 2) 图形不对称右偏  2）一般我们认为价格服从对数正态分布 log-normal, 但是收益率服从正态分布 normal

第四种 student‘ s t-distribution(T-分布）

参数只有一个： 自由度（df) --能够自由变动的变量个数。

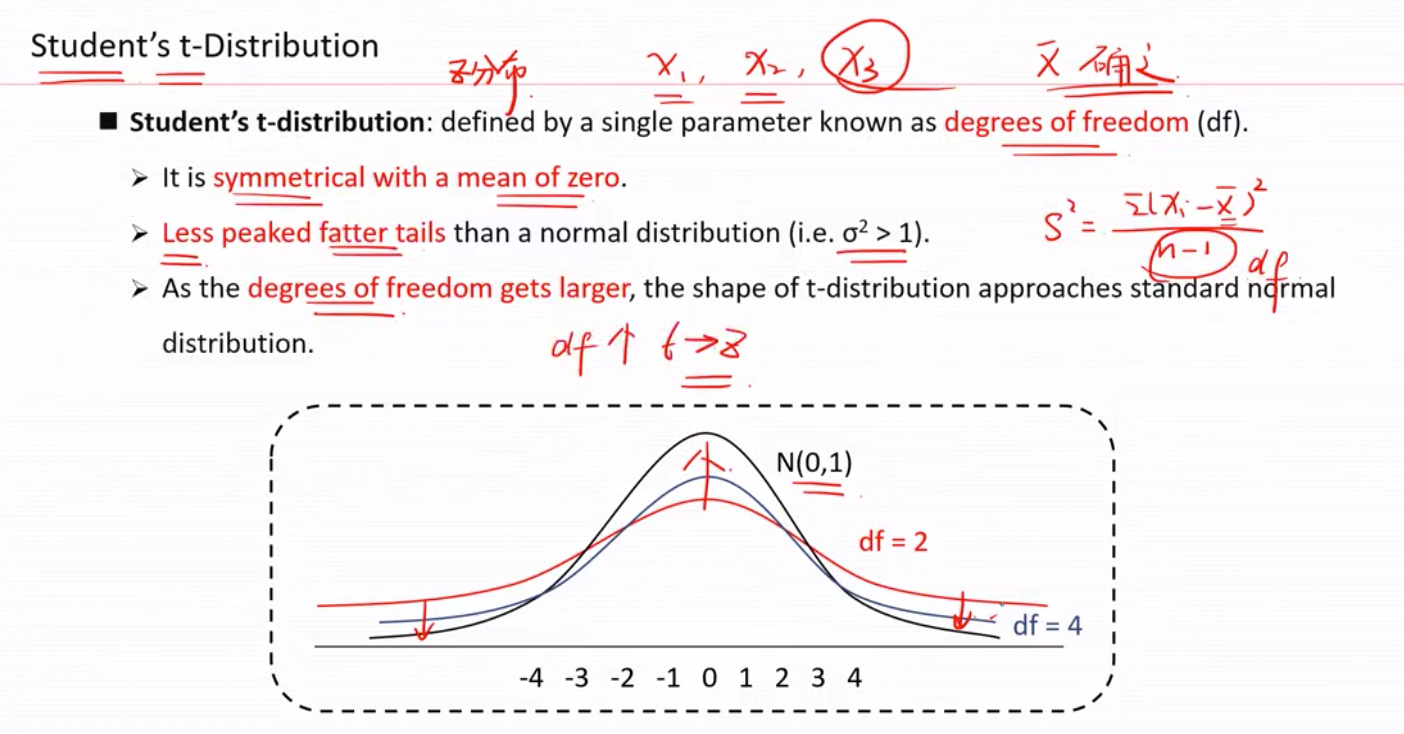
t-分布 vs z -分布（标准正态分布）

性质1: 都会以0 对称

性质2: 相比标准正态分布，尾巴更加肥，z分布的方差是1 ， 所以t 分布的方差必然>1

性质3，随着自由度（df-能够自由变动的变量个数)增加，形状越接近于标准正态分布

当自由度=8 是 t 分布和z 分布非常相似了

第五种，chi-squrare distribution 

第六种 f-分布

蒙特卡洛模拟

用input 的因素（x, y, z)的分布 随机抽样值带入函数，得到output的分布,重复如此抽样n 次 ，统计得出的output 的分布。

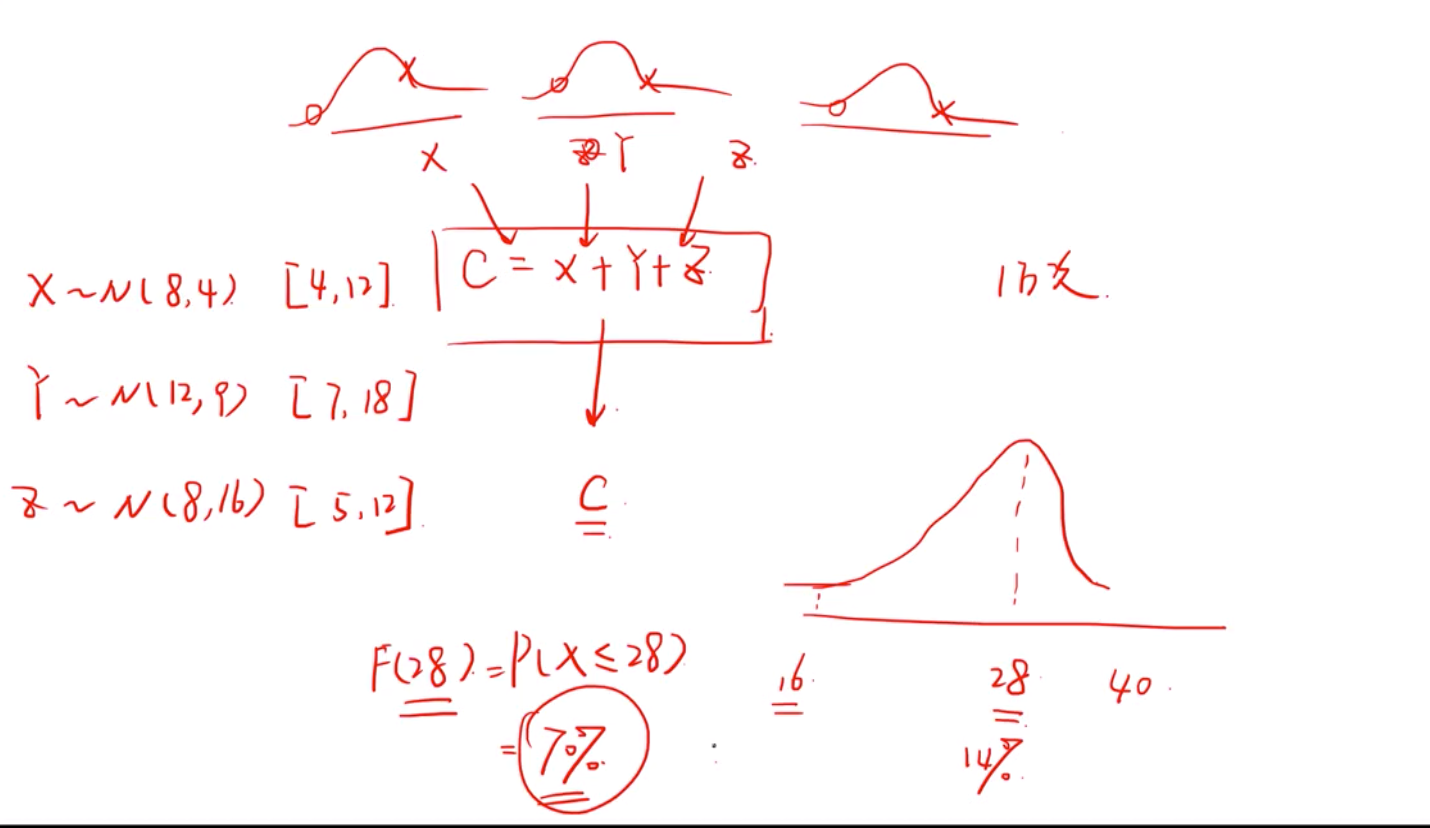
常用来预测一个公司的股价，用input 的分布来得到output的分布。这是一种重要的思想。

离散均匀分布、二项分布、连续均匀分布、正态分布、对数正态分布，t分布、卡方分布，f 分布 ，蒙特卡洛模拟