多元线性回归

线性方程等式要加尖嘴cap 

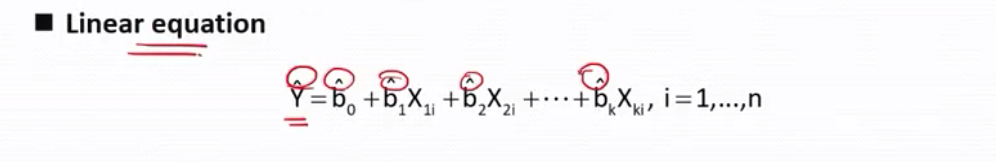
b0 --截距

斜率--偏斜率-它表示在其他自变量不变的情况下，该自变量对y 结果的影响。

几个比较重要的假设，下面3个打勾的假设。所以后面我们要重点对这几个假设做检验。

条件异方差是指残差项和x的取值是有关系。非条件异方差是没有关系的，我们要担心的是条件异方差，所以我们有下面的方式来检验是不是条件异方差。

如果reject H0，则 说明确实存在条件已发差。那么问题了，那么他是正序列相关呢还是负序列相关？

正序列相关定义： 如果前一个是正，那么下一个也极有可能是正的，或者 如果前一个是负，那么下一个也极有可能是负的， 

负序列相关定义： 如果前一个是正，那么下一个也极有可能是负的，或者 如果前一个是负，那么下一个也极有可能是正的，

经济情况通常正序列相关更多些。比如，通涨影响往往持续一段时间，而不是上下跳动的。 

关于序列相关的检验我们有dw -test 

dl=low du-upper , 查DW  表得知dl and du值。

落在（0～dl ) 或者（4-dl~4) 就相当于r 落在 (dl~1 ) 或（4-dl~-1) , 表名假设检验量 r 非常强的正或负相关性。

多重共线性，通常多因素之间多少都会有，但是各因素的线性关系不是很明显的话，我们一般也可以接受。

多余多重共线性，没有固定的检验方法，我们一般对各个因素（自变量）之间两两比较他们的相关性系数，如果该系数非常接近1 或-1 就表明这两个自变量之间非常有线性关系。如果这样的话，去掉其中一个自变量就可以了。

对假设前提的检验

对一元线性回归要检验斜率是否为0 ，那么对于多元线性回归就要对每一个自变量的斜率是否为0做检验。

除此之外，还有做一个联合假设

当msr>>mse 才会落在右边的拒绝域