sql=select item, value from tfinance_yahoo where corp="MSFT" and period="2020
df1=pd.read_sql(sql, con=con)
11:45分运行
a=[1,2,3]
c=list(a)
c is a
Out[91]: False
a is c
Out[92]: False
用==就是true
is的比较不是一个东西(类型),值(内容)一样也是false
==的比较(等于),值一样则为true

ANONA-Analysis of Variane




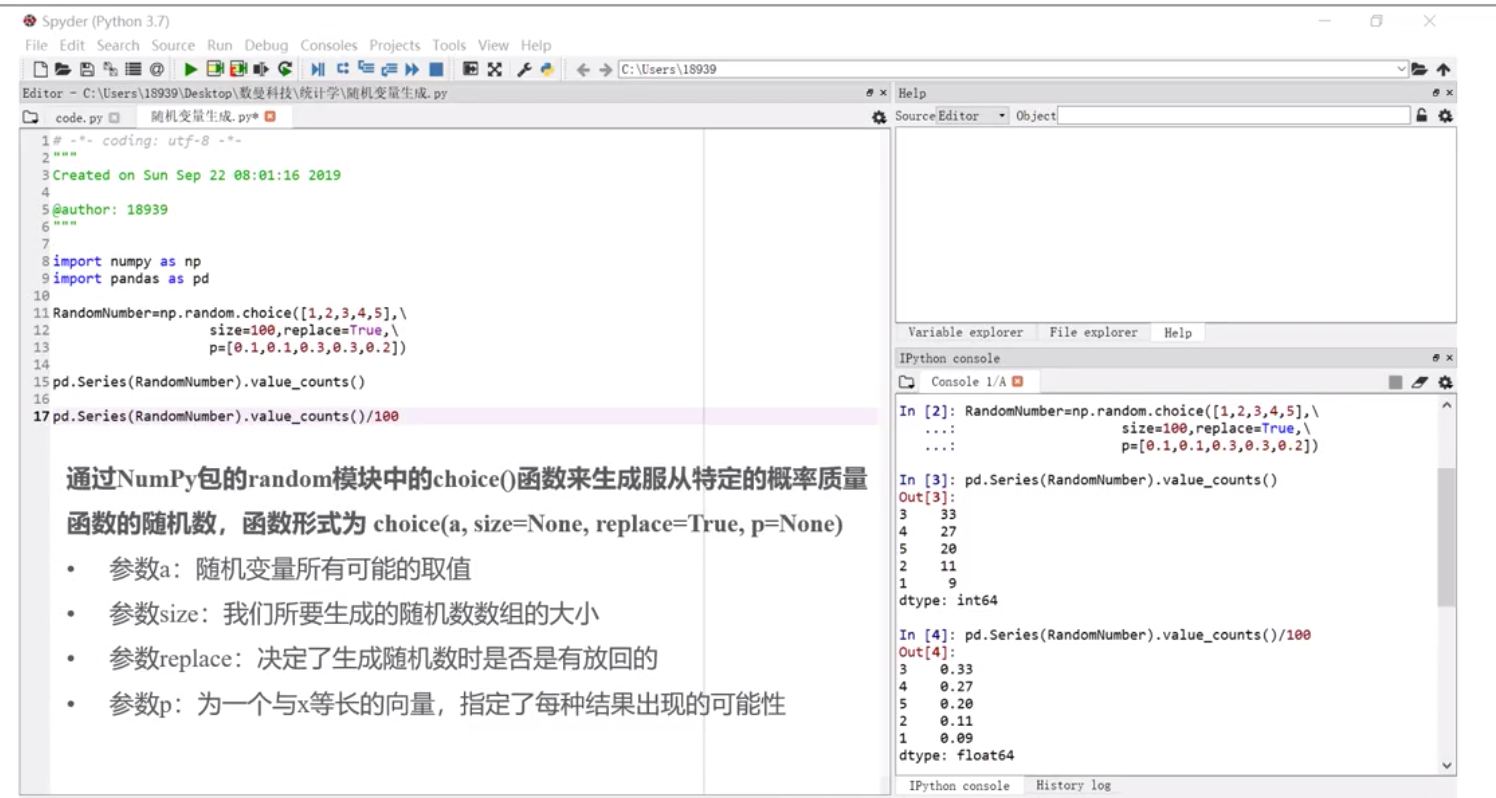
 收益率、价格都是连续性随机变量
收益率、价格都是连续性随机变量

利用numpy 库的random.choice()



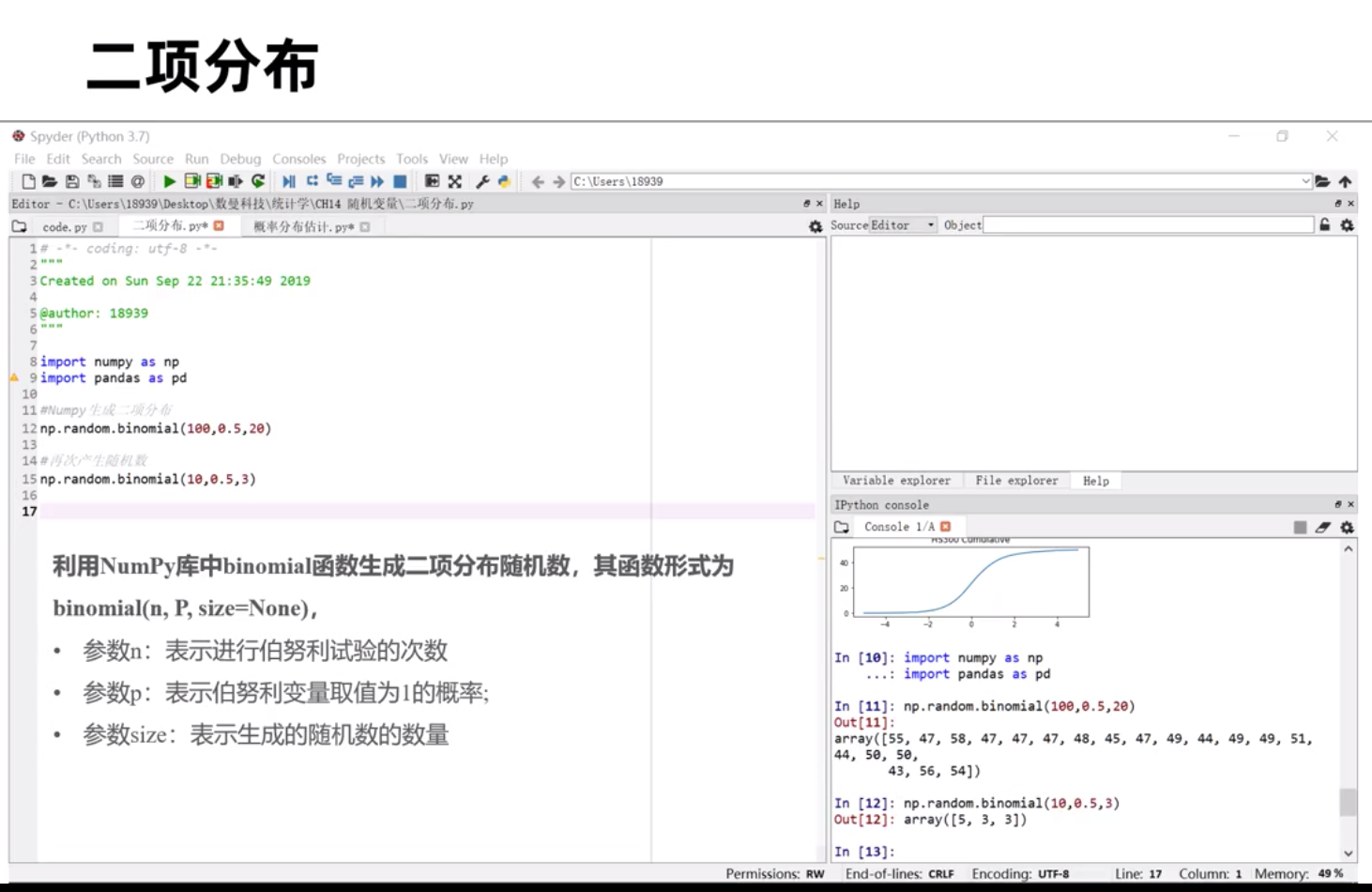

二项分布常常有来预测股价上涨或下跌,这两种结果的概率。比如从历史数据中知道过去100天中沪深300指数上涨的概率为0.53 ,那么求在10个交易日中有6天上涨的概率?就可以用二项伯努利pmf函数来求得。



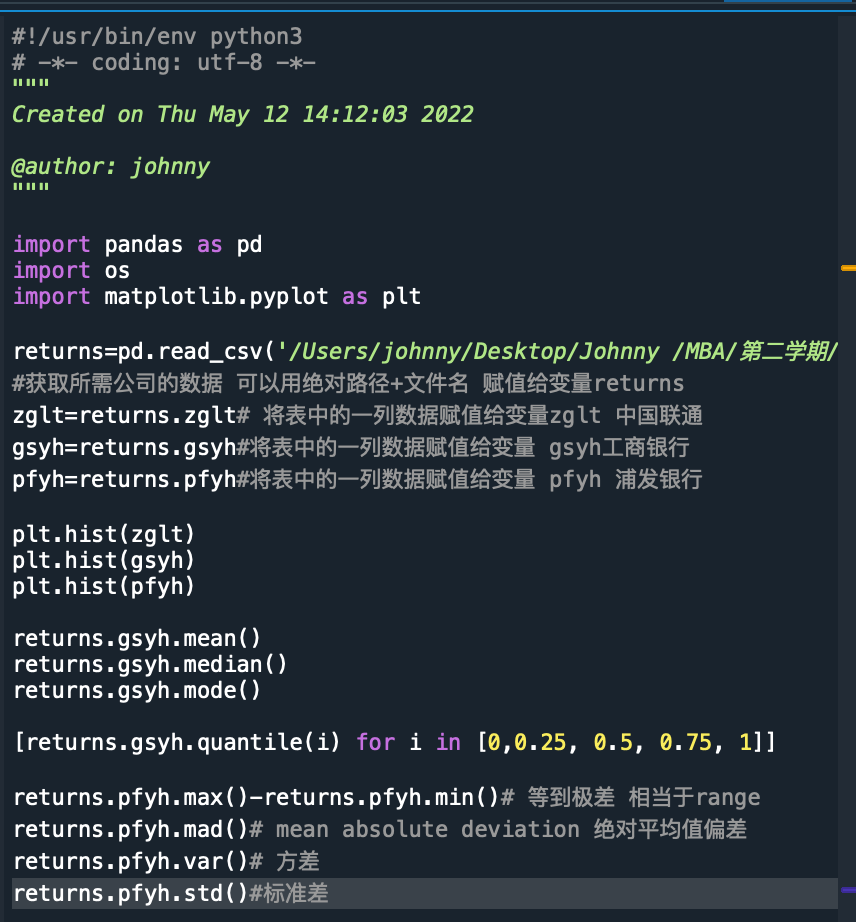

MAD()==mean Absolute Deviation
[returns.gsyh.quantile(i) for i in [0.25, 0.5, 0.75]]
多元线性回归

线性方程等式要加尖嘴cap
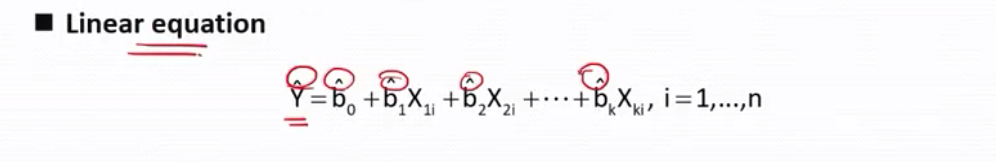
b0 --截距

斜率--偏斜率-它表示在其他自变量不变的情况下,该自变量对y 结果的影响。
几个比较重要的假设,下面3个打勾的假设。所以后面我们要重点对这几个假设做检验。


条件异方差是指残差项和x的取值是有关系。非条件异方差是没有关系的,我们要担心的是条件异方差,所以我们有下面的方式来检验是不是条件异方差。

如果reject H0,则 说明确实存在条件已发差。那么问题了,那么他是正序列相关呢还是负序列相关?
正序列相关定义: 如果前一个是正,那么下一个也极有可能是正的,或者 如果前一个是负,那么下一个也极有可能是负的,
负序列相关定义: 如果前一个是正,那么下一个也极有可能是负的,或者 如果前一个是负,那么下一个也极有可能是正的,
经济情况通常正序列相关更多些。比如,通涨影响往往持续一段时间,而不是上下跳动的。
关于序列相关的检验我们有dw -test

dl=low du-upper , 查DW 表得知dl and du值。
落在(0~dl ) 或者(4-dl~4) 就相当于r 落在 (dl~1 ) 或(4-dl~-1) , 表名假设检验量 r 非常强的正或负相关性。
多重共线性,通常多因素之间多少都会有,但是各因素的线性关系不是很明显的话,我们一般也可以接受。
多余多重共线性,没有固定的检验方法,我们一般对各个因素(自变量)之间两两比较他们的相关性系数,如果该系数非常接近1 或-1 就表明这两个自变量之间非常有线性关系。如果这样的话,去掉其中一个自变量就可以了。
对假设前提的检验

对一元线性回归要检验斜率是否为0 ,那么对于多元线性回归就要对每一个自变量的斜率是否为0做检验。

除此之外,还有做一个联合假设



当msr>>mse 才会落在右边的拒绝域

回归分析 vs 方差分析
方差分析
回归分析. X 数值型, Y数值型
既然x, y 都是数值型,就可以得到一个方程来做预测。


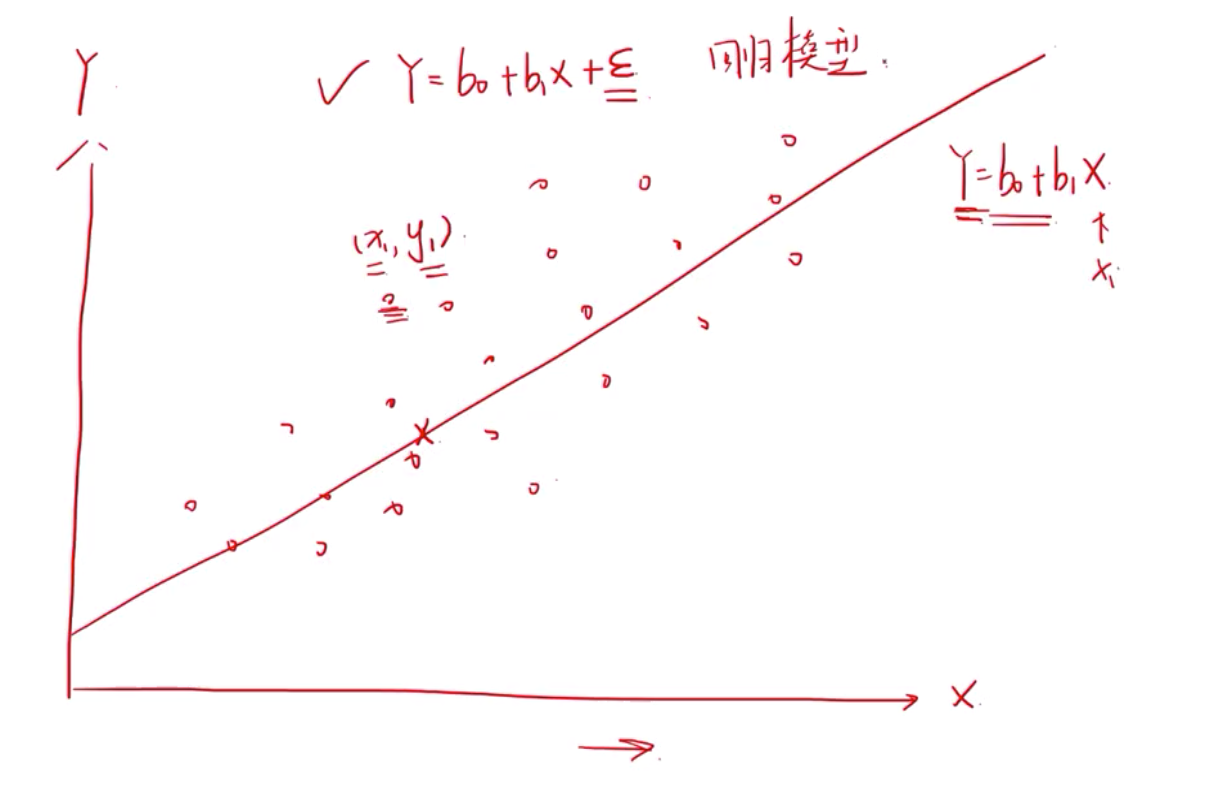
有残差项(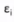 )的才叫回归模型
)的才叫回归模型
这条拟合线就是残差项的平方加起来最小的线
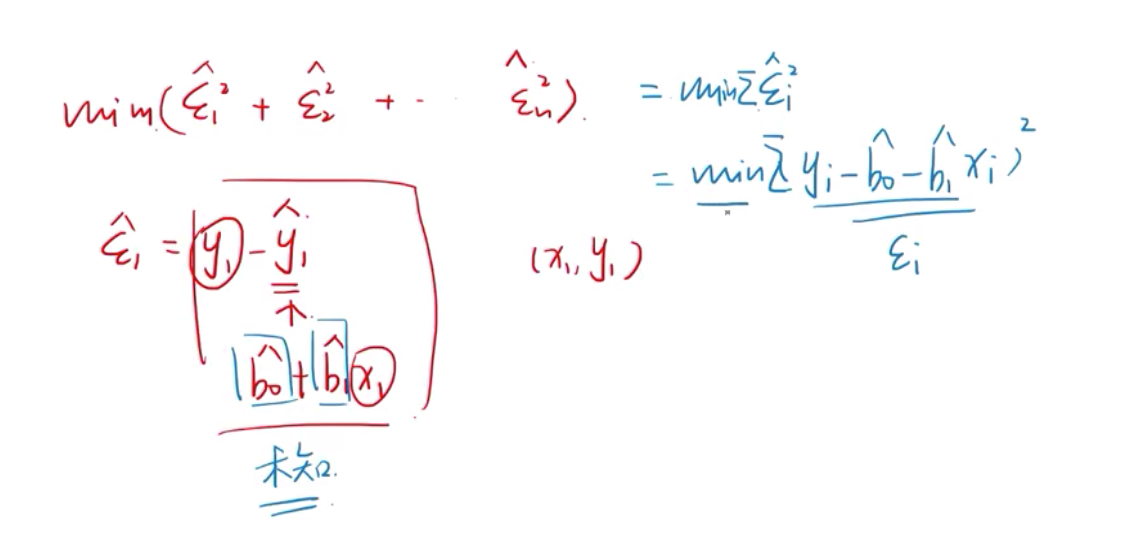



一元线性回归的前提条件:
两者有线性关系(散点图货假设检验)

重点解释一下第三条

找到回归系数后,我们哟做分析来确定找到的b1,b0 是不是靠谱。
我们最当心的就是斜率b1=0, 如果是就表示y和x之间根本就没有线性关系,所以要假设h0: b1=0 来做假设检验。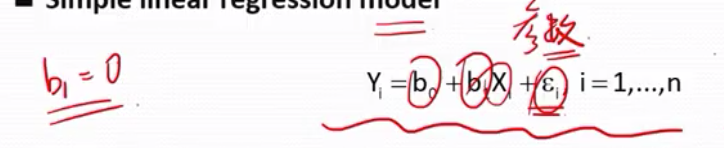



R2 是一个相对指标,选一个R2最大的即可。
方差分析(anlysis of variance) 有什么用? 答:方差分析是用来发现两个或多个变量之间的关系的.
方差分析不是用来告诉我们自变量和应变量之间的等量关系的,而是告诉我们分类型自变量之间的关系是否显著
其中分为单因素分析 和双因素分析,其中双因素分析中分为自变量之间无相互关系和两个自变量间有相互关系两种情况。
展开来讲:
单因素分析
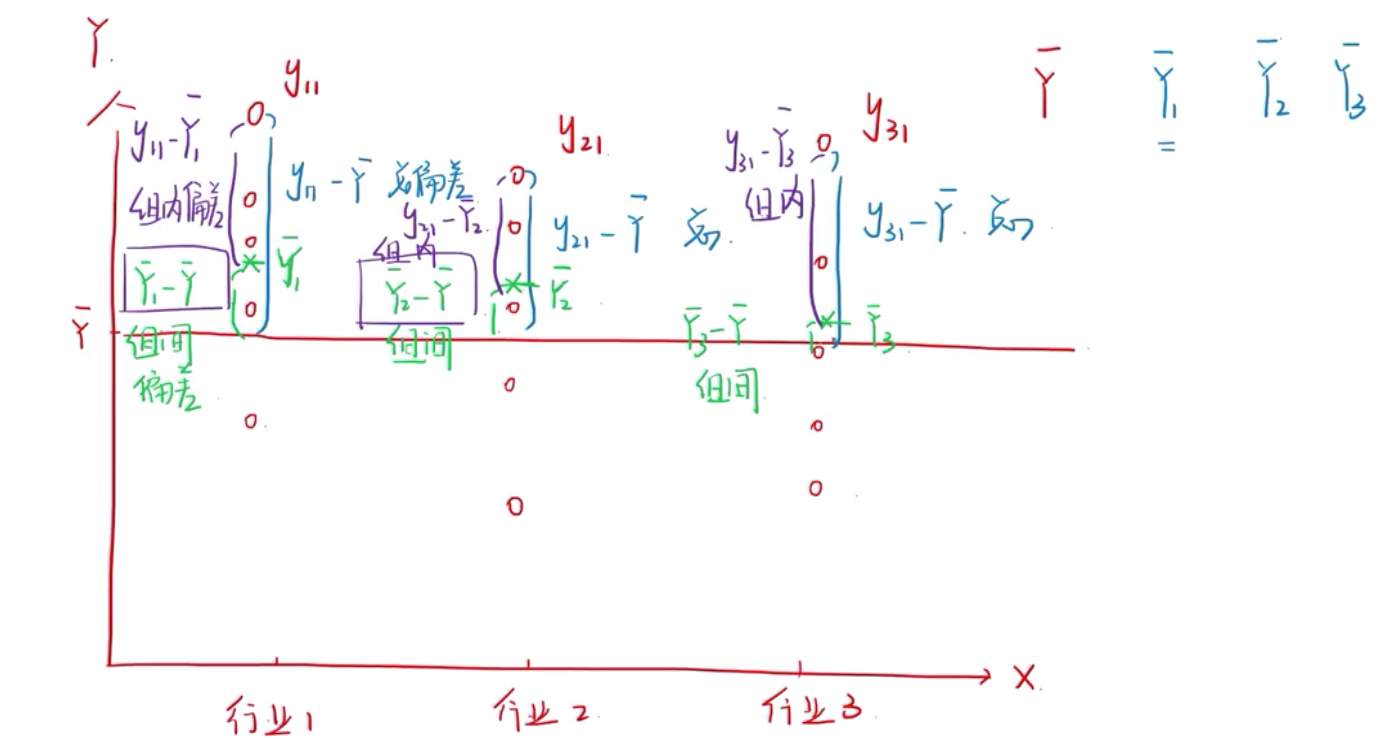
发差分析的原理就是看数据波动(离散)的来源。
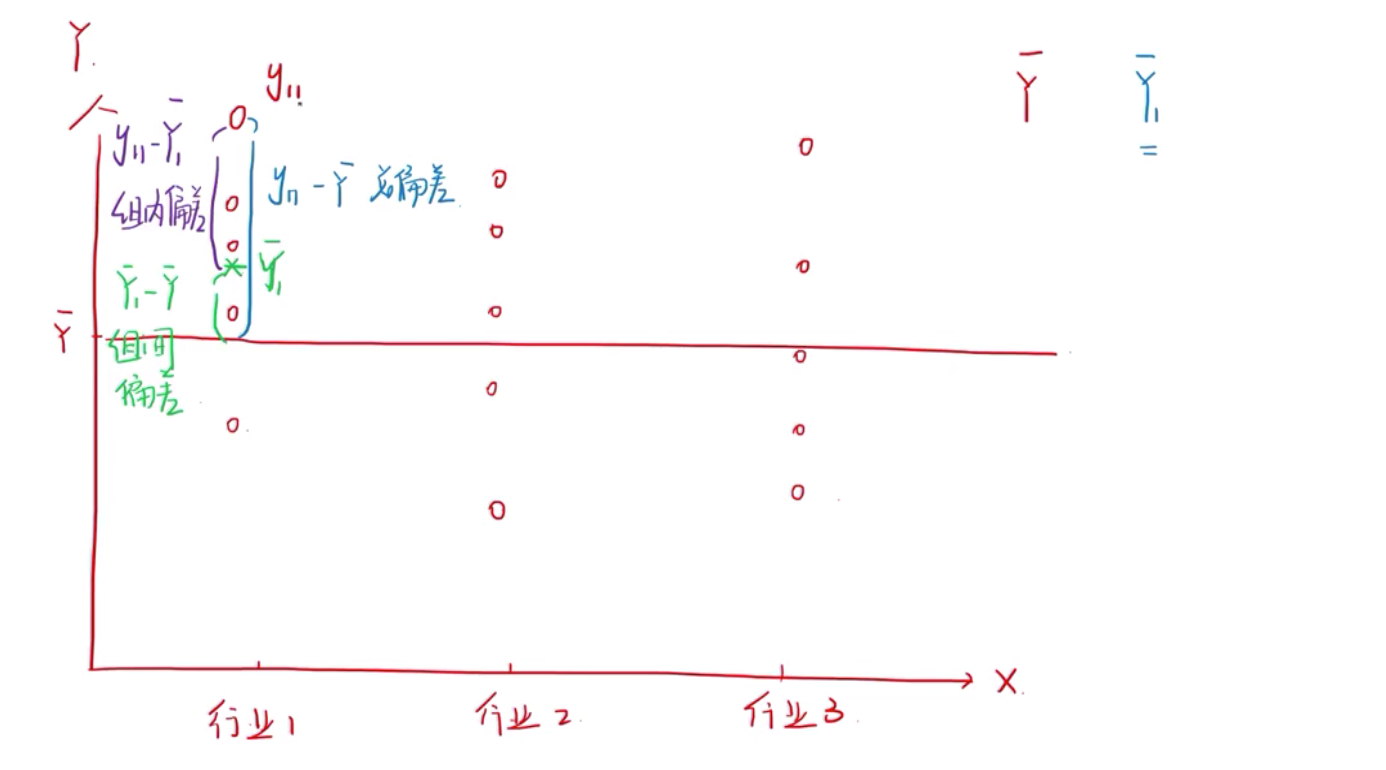
组间偏差(绿色)+组内偏差(紫色)=总偏差(蓝色)

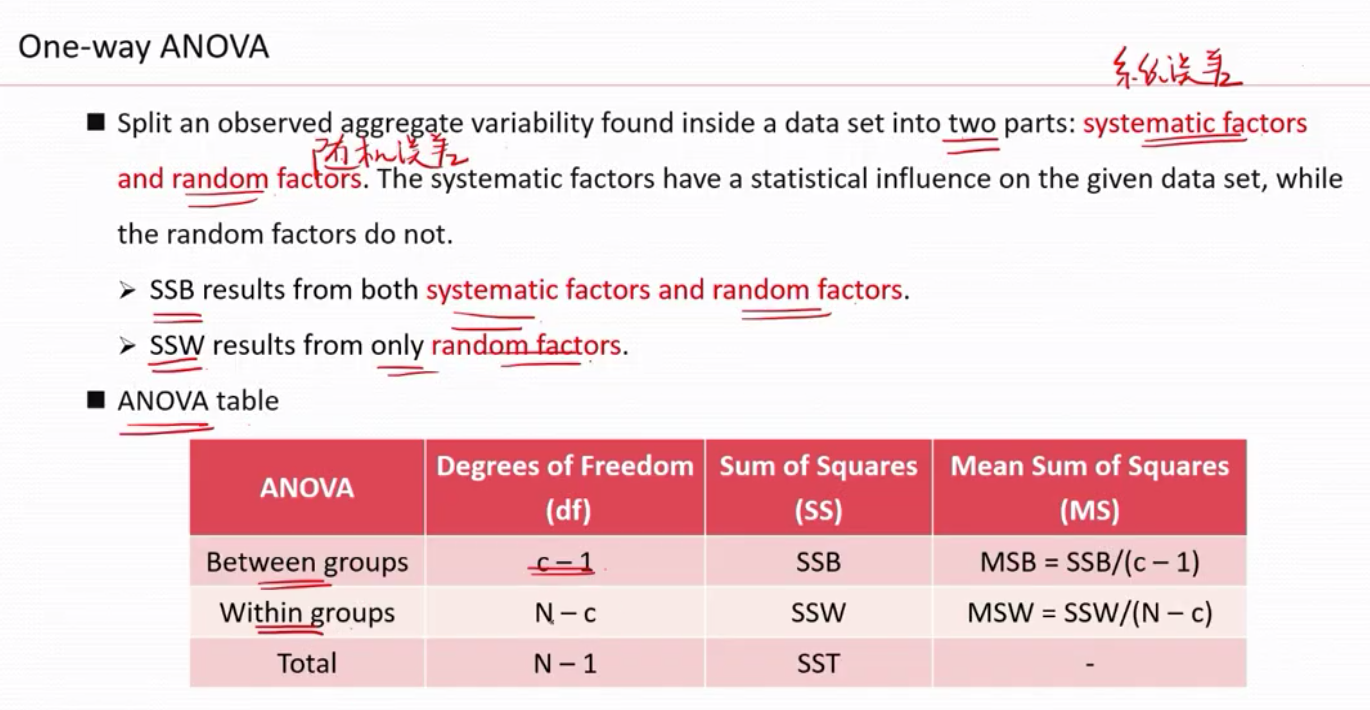
方差分析ANOVA 认为有两个因素导致了误差(系统误差)和(随机误差)




单因素方差分析的假设检验的前提:

双因素方差分析(无交互影响的状况)



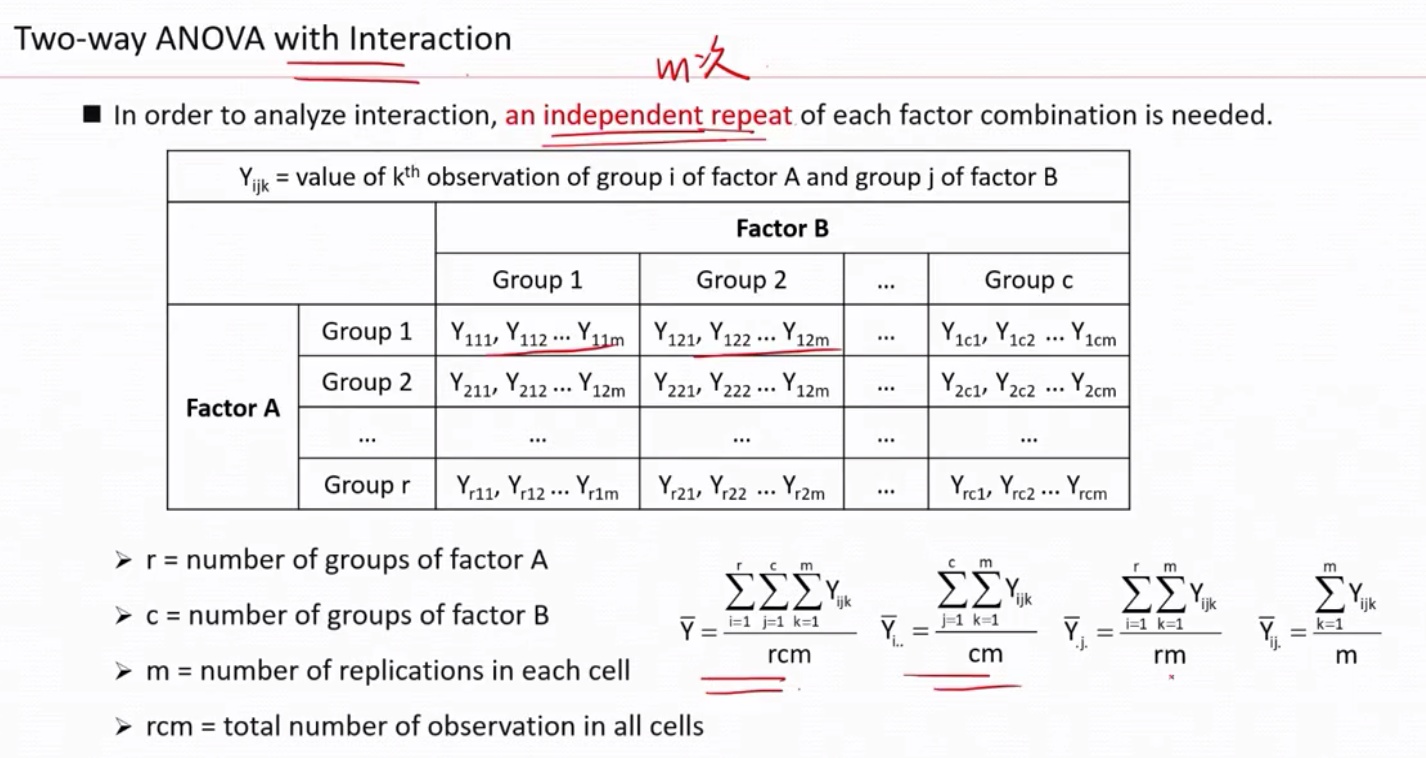
双因素方差分析(有交互影响的状况)
相当于在无交互影响的状况从单次抽样变成多次(m次)抽样



type I error --去真(错杀),小概率事件发生的概率是多少?就是显著性水平alpha,相反,H0 是真的,又没有被我reject的概率就是1-alpha=confidence level
type ii error --存伪,H0 is false, but we do not reject , we call it as beta , therefore, 1-beta is power of test (检验力度)
一般来讲这两类错误是此消彼长的。
但是如果增加样本数量可以同时降低这两类错误,因为,这两类错误来源于抽样,如果抽样数量越接近总体,则这两类错误就越来越小了
 假设检验单个总体均值,用上图
假设检验单个总体均值,用上图
如果要假设检验两个总体均值,则有几个前提条件,总体必须是正态分布(t 分布),总体的方差虽然未知但是要相等才能做假设检验。
如果是独立样本用下面的方法

第一步, 假设
第二步, 确定分布类型及公式
第三步,画分布图找出拒绝域、
第四步,找到关键值,查表等tc
第五步,抽样去计算样本均值,带入公式计算
第六步,如果落在拒绝域内,就reject H0, 否则,我们不能拒绝h0 假设。
如果是非独立样本(paired comparsions test)用下面的方法

比较两个公司的收益率的差异


方差的检验
单个方差的检验(卡方分布)

两个独立样本的方差相等检验

两个样本的相关性(检验是否有线性相关性)h0: 线性无关,h1, 线性相关

6种检验的总结


第二部分 假设检验(先猜后证)
先假设后抽样来验证。

基本原理,小概率事件不会发生
先假设,然后抽样验证
中心极限定理-> 复合正态分布,标准化后得到z 分布, 然后看下我的随机抽样落在小概率区间(显著性水平)范围内,如果是, 那么唯一的解释就是我的原假设错了。假设检验的基本原理是认为小概率事件不会发生。
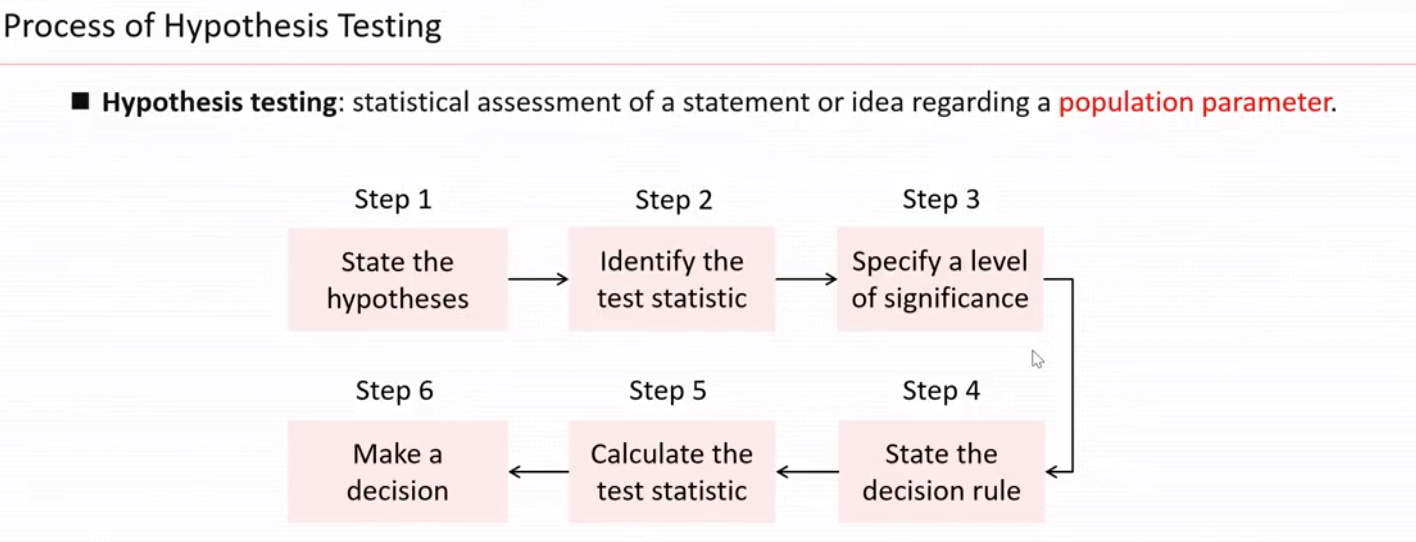
假设检验的步骤

h0 原假设 有等于=号的。Ha 备择假设 。比如
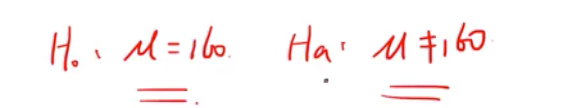
注意, h0 原假设,Ha 备择假设必须是互斥并且它们是遍历所有可能的。



画出拒绝域(单尾,双尾)
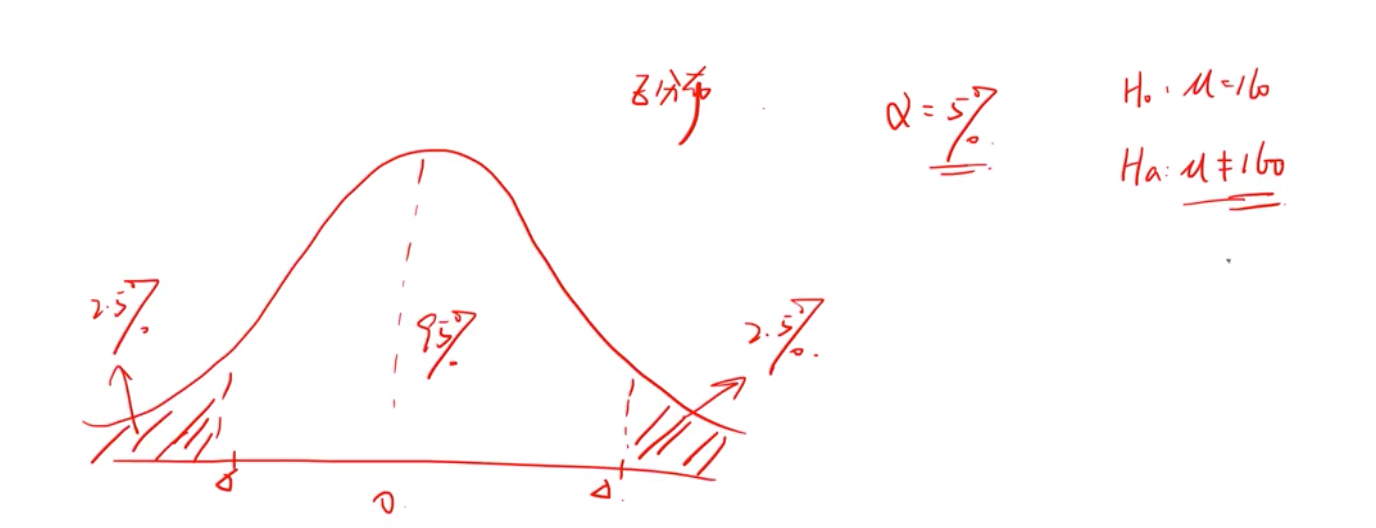
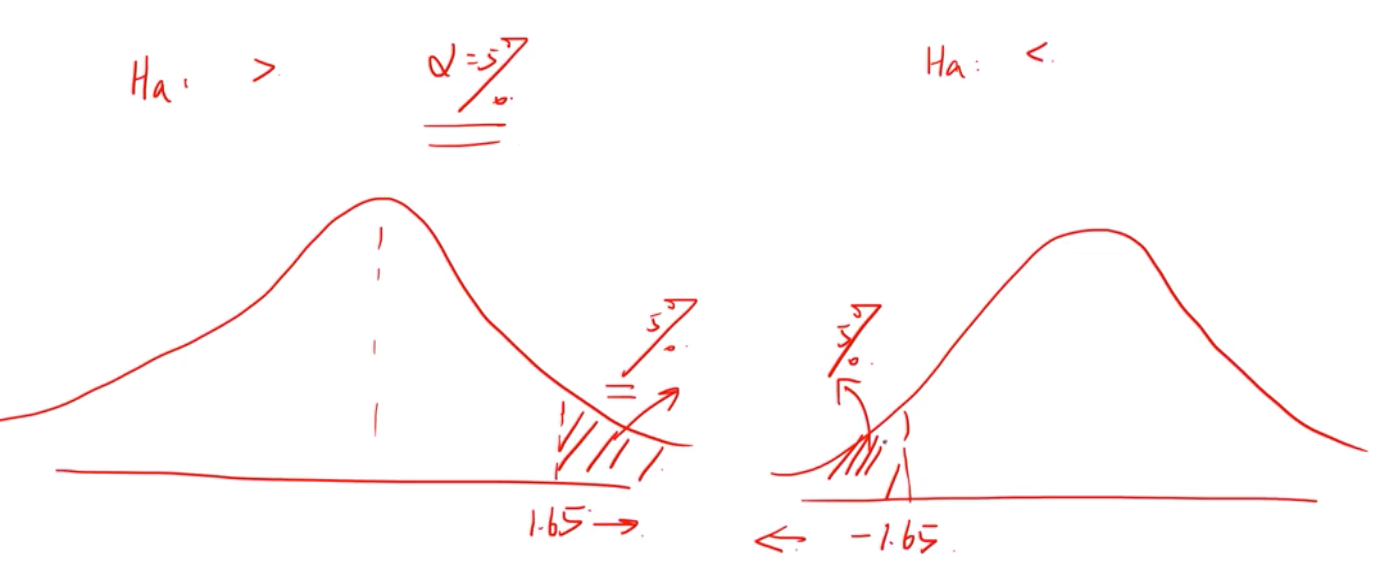

Alpha显著性水平是自己定的
step5 , 计算出p-value 用来和alpha 比较。

p-value <alpha ,reject H0

注意,step6 我们拒接原假设或者不能拒绝原假设两种,这叫严谨。
推断性统计有两个分支
1. 估计 2 假设性检验
第一部分, 估计, 就是用样本来估计总体的情况

注意总体和样本的符号是不同的, 总体的参数通常用希腊字母表示,样本参数通常用英文字母表示
凡事样本抽样都是随机变量 都有一个概率分布

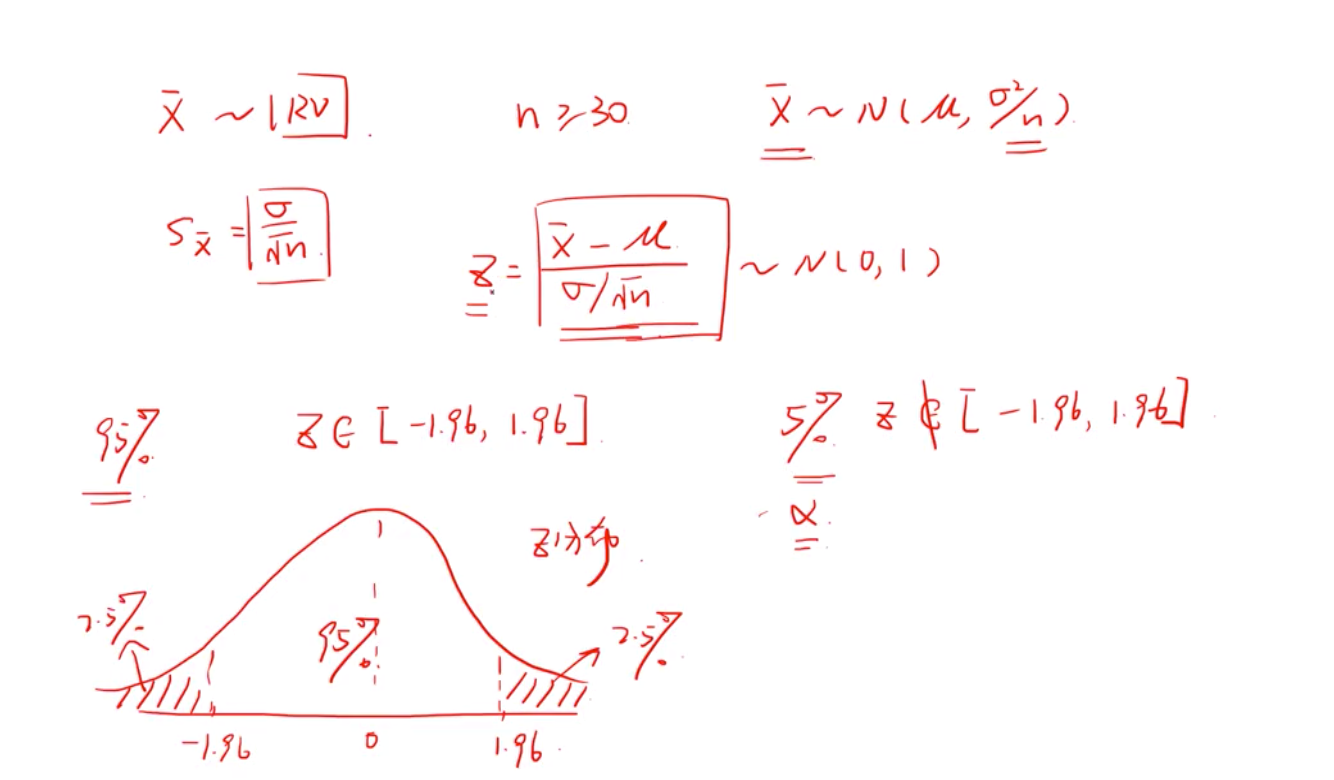
中心极限定理告诉我们当样本容量n>=30 且总体均值和方差已知的常数的情况下,那么样本就会近似符合正态分布。而且这个样本的均值和总体的均值是一样的,样本的方差等于总体方差除于n .比如,全国人口的身高,就会复合正态分布的常数。

标准误--指样本均值的标准差
已知总体方差的情况和未知总体方差的情况分开讨论如下:

注意 在未知总体方差的情况洗, 不知道总体标准差值![]() , 所以只能用样本标准差s 代替, s 则来自于
, 所以只能用样本标准差s 代替, s 则来自于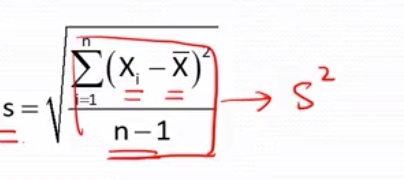 ,要注意, 样本的标准差s 和所求的样本均值的标准差
,要注意, 样本的标准差s 和所求的样本均值的标准差![]() 是两个不同的概念。
是两个不同的概念。

如何用样本来估计总体的均值有两个办法。
第一种,点估计 (单次抽样-不太靠谱);
第二种,区间估计(给出一定的区间范围以及落在该范围内的概率confidence level)-比较靠谱

那么这个范围如何来确定呢?
要分为 总体的方差已知和总体方差未知两种情况来讨论。
第一种,
由中心极限定理知道样本大于30的样本分布类似于正态分布,第二部,标准化成标准正态分布,即得到一个z 分布。如下:
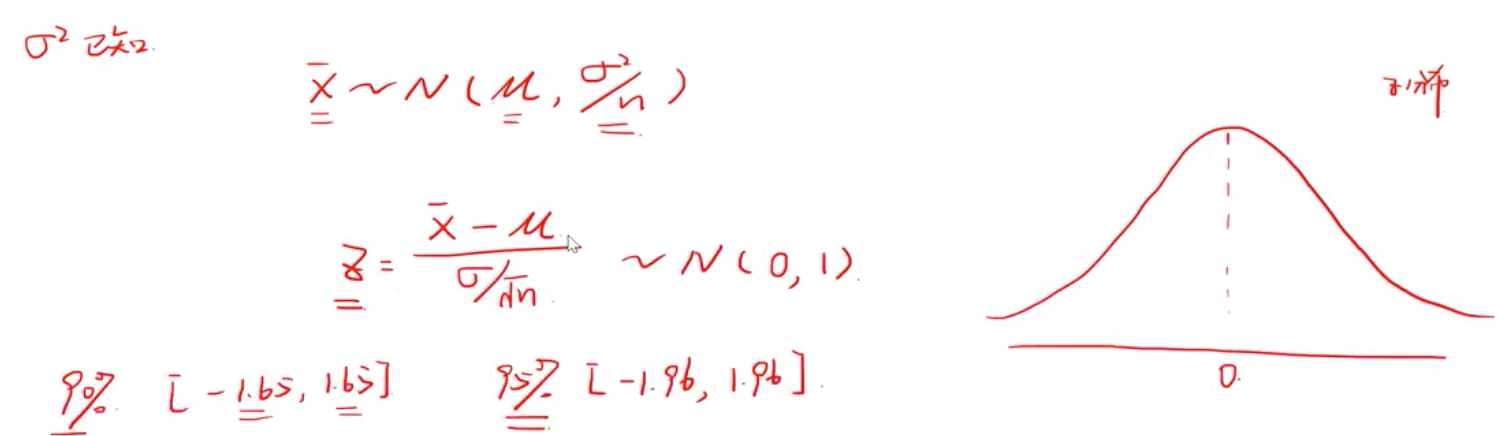
要记住的是
1.65,1.96 代表 confidence level 90%, 95% 的概率,取值会落在该区间。
另外, 相对于90%,95% CL 剩下的10%,5%我们称之为显著性水平alpha ![]() 即下图,绿色阴影部分。
即下图,绿色阴影部分。
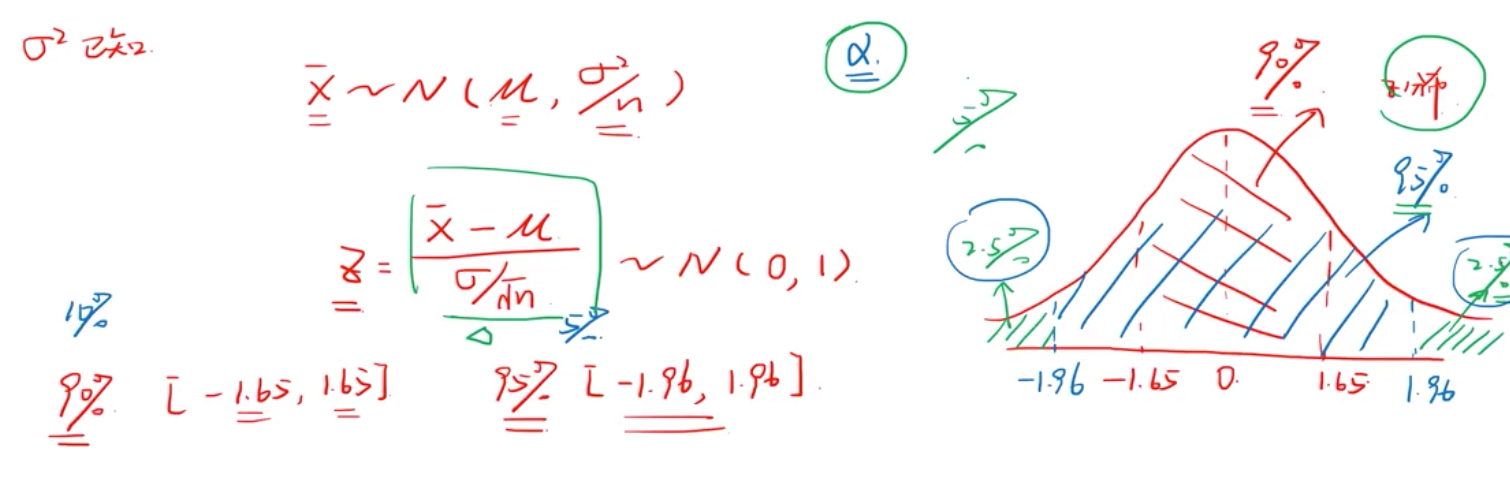
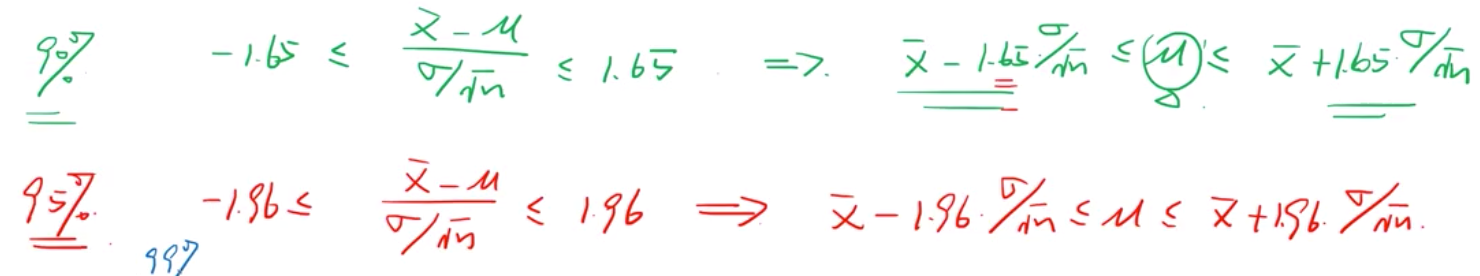
第二种情况 在总体方差未知的情况下
现在抽样的均值和抽样的方差两个都是随机变量,出现了不值一个随机变量的这种情况下,那么样本就不在服从正态分布了,而是服从t-分布。
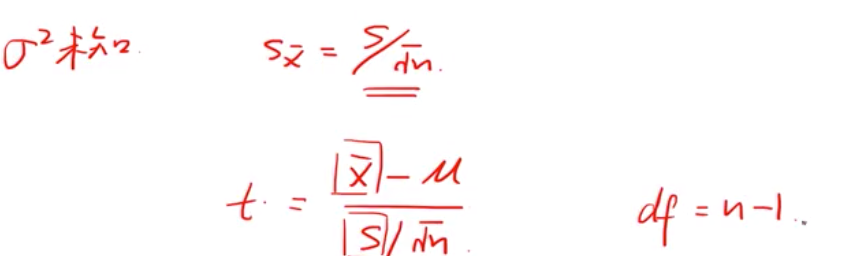
t-分布相比z -分布,它的形状是低峰肥尾的。那么t-分布的关键值就是不一样的。查t-分布表可得到。




第三种: 连续均匀分布
1) 在某一个区间内去到某值的概率为0

2)正态分布 normal distribution
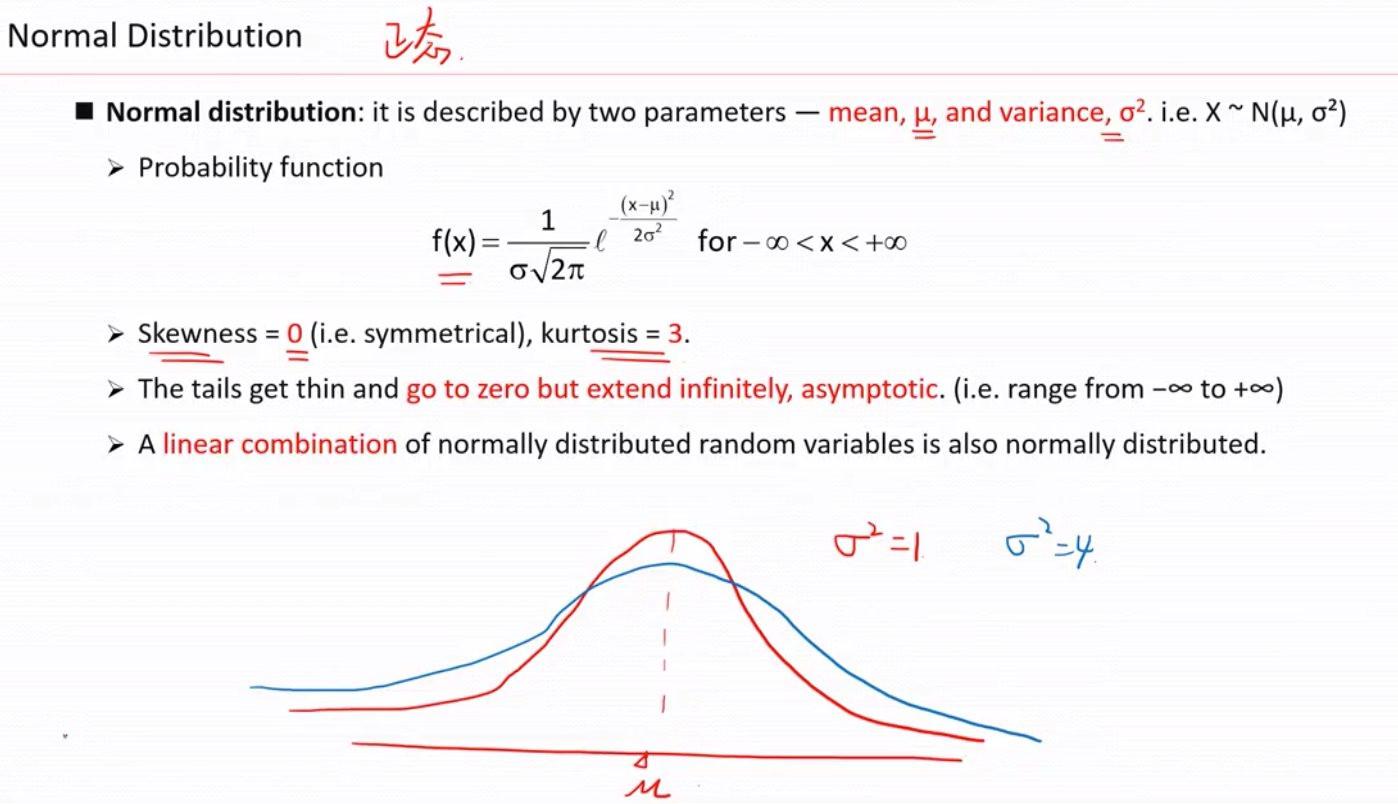
正态分布的3个性质
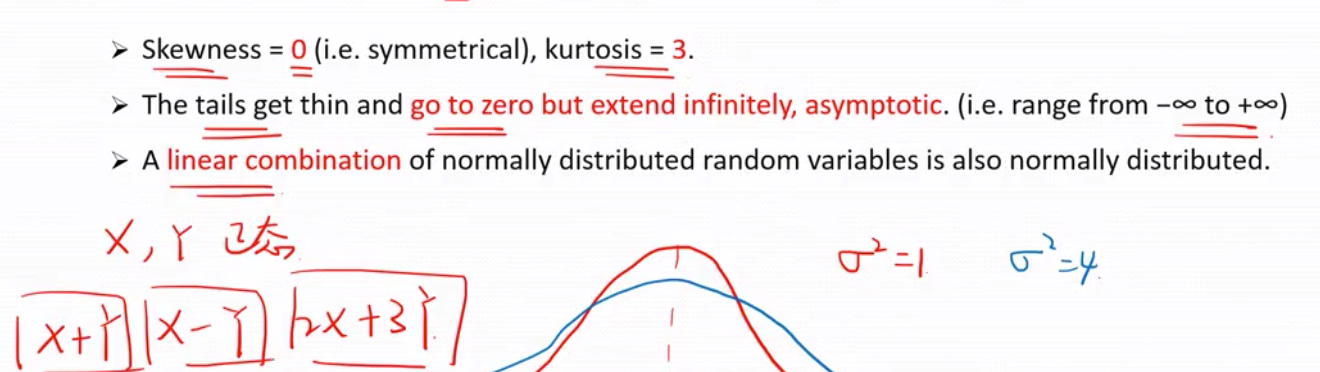
1)偏度为 0 ,峰度为3
2)长尾无限趋近于0单不等于0 , 即范围是负无穷到正无穷
3)服从正态分布的几个随机变量的线性表达式也符合正态分布
置信区间--对于服从正态分布,反映的是落在1倍,1.65倍,1.96倍,2.58倍标准差的区间的概率 68%,90%,95%,99% (常用这几个)
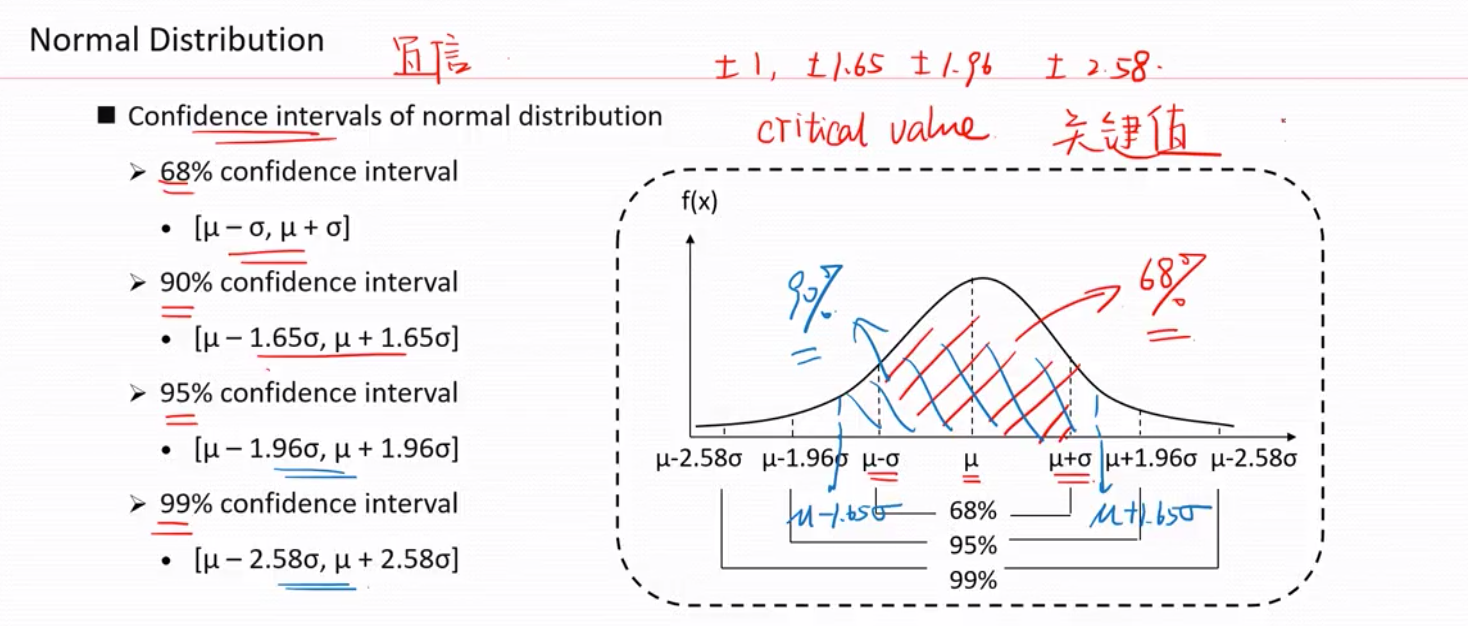
正态分布标准化后得到标准正态分布,通常用z 表示,故又称 z 分布

1,1.65,1.96, 2.58 是置信区间的关键值(临界值)常用要背。
第四种: 对数正态分布 log normal distribution
对数正态分布的性质
1) 取值必须>0 2) 图形不对称右偏 2)一般我们认为价格服从对数正态分布 log-normal, 但是收益率服从正态分布 normal
第四种 student‘ s t-distribution(T-分布)
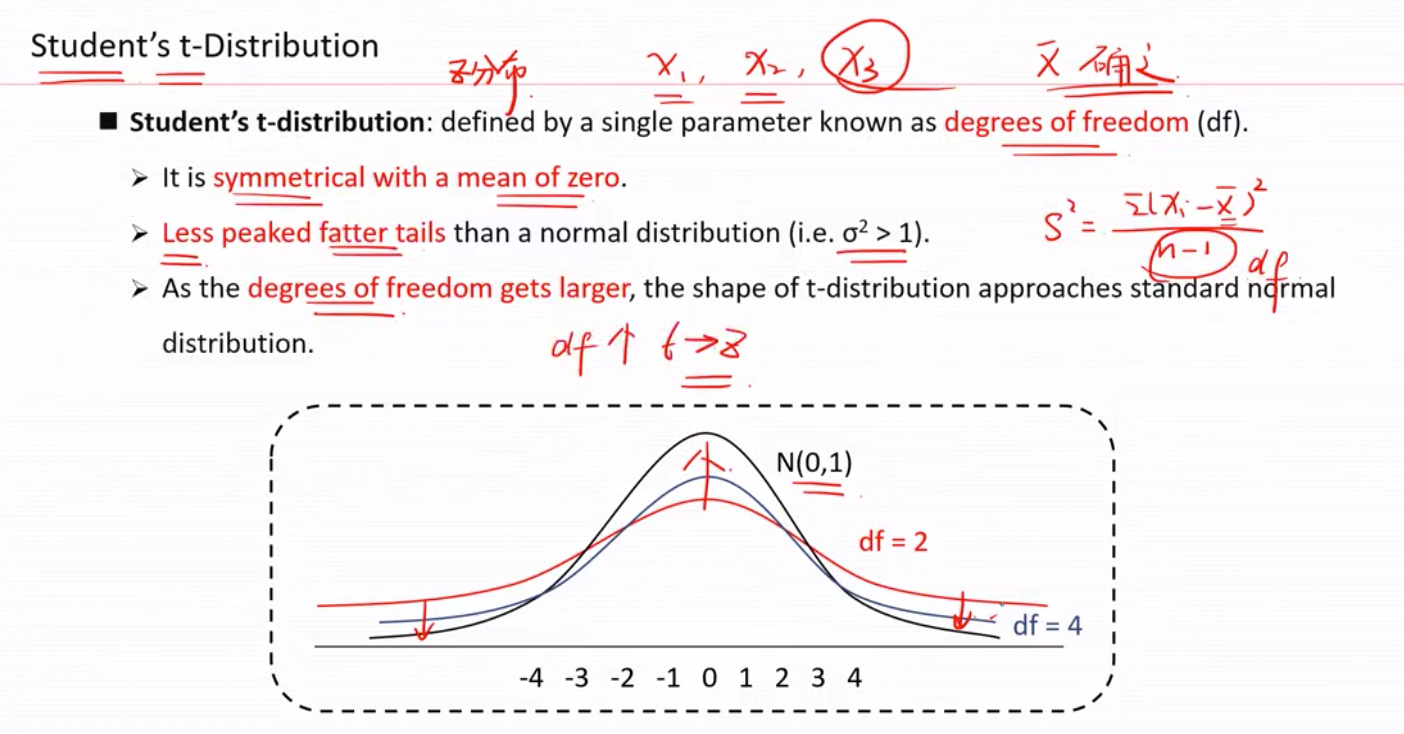
参数只有一个: 自由度(df) --能够自由变动的变量个数。
t-分布 vs z -分布(标准正态分布)
性质1: 都会以0 对称
性质2: 相比标准正态分布,尾巴更加肥,z分布的方差是1 , 所以t 分布的方差必然>1
性质3,随着自由度(df-能够自由变动的变量个数)增加,形状越接近于标准正态分布
当自由度=8 是 t 分布和z 分布非常相似了
第五种,chi-squrare distribution
第六种 f-分布

蒙特卡洛模拟

用input 的因素(x, y, z)的分布 随机抽样值带入函数,得到output的分布,重复如此抽样n 次 ,统计得出的output 的分布。
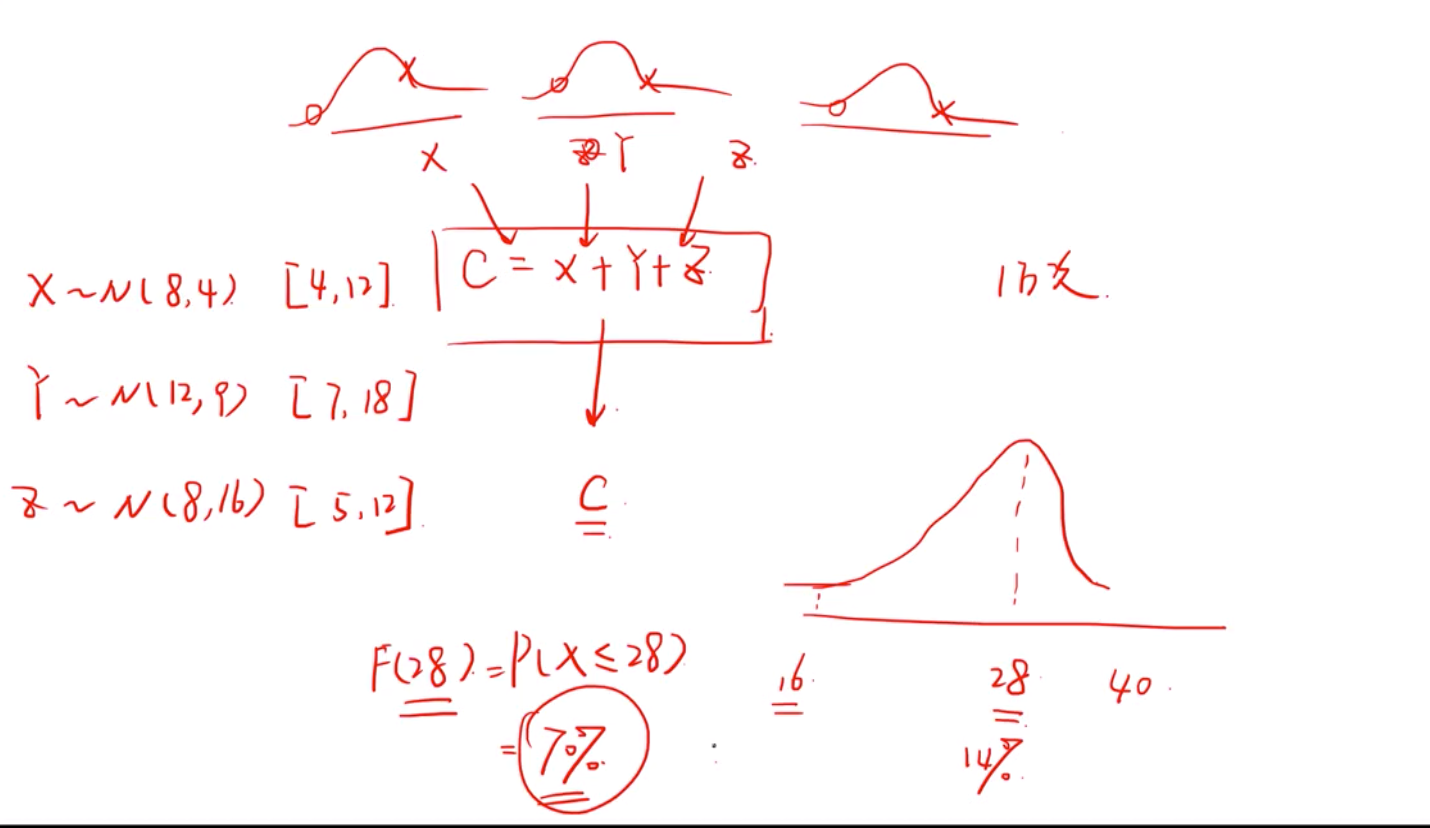
常用来预测一个公司的股价,用input 的分布来得到output的分布。这是一种重要的思想。

离散均匀分布、二项分布、连续均匀分布、正态分布、对数正态分布,t分布、卡方分布,f 分布 ,蒙特卡洛模拟

这个章节我们要学习7种重要的的分布--the uniform, binomial, normal , lognormal , student's t, chi-square, F-distribution


1) 离散随机变量。如骰子
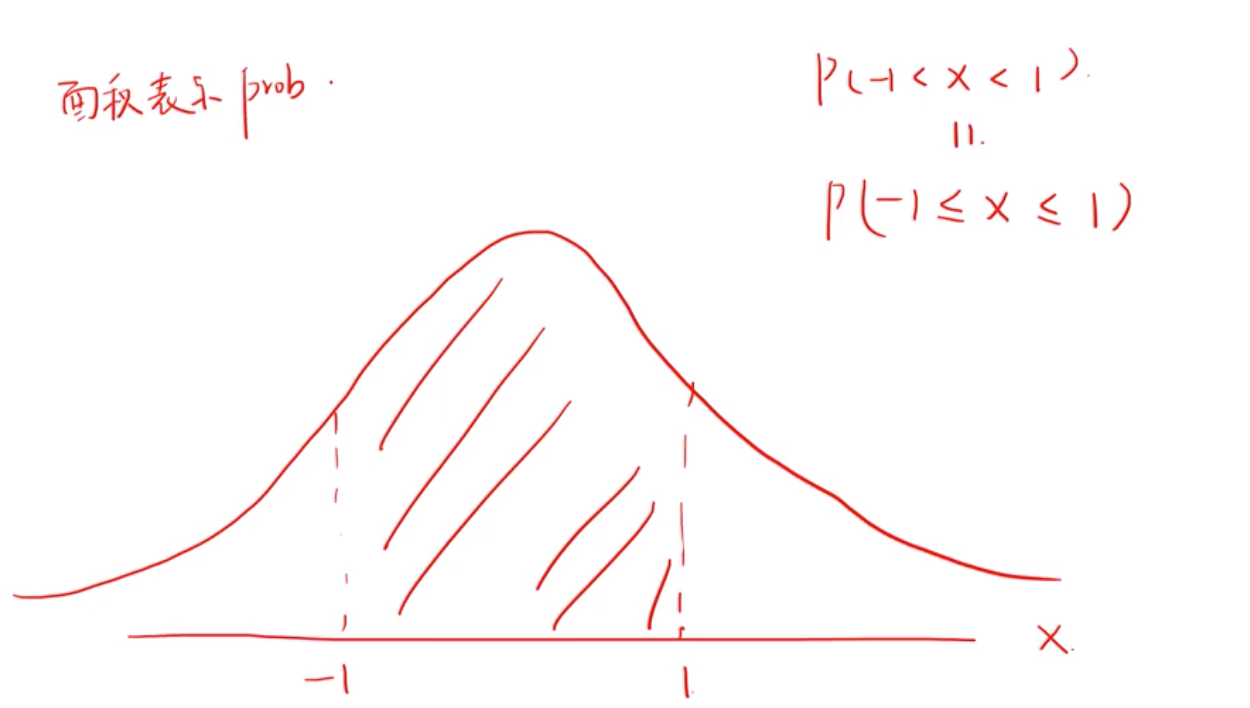
2)凡事连续的随机变量,不管能不能取到这个值,它的概率都是0, P(x)=0 even though x can occur. 正因为如此,我们只能退而求其次,取该值附近的值的概率。也称为概率密度函数pdf, 举例, 正态分布是连续的随机变量,所以,有没有等于好,面积一样,寄概率一样。
第一种,离散均匀分布,discrete uniform distribution

第二种,二项离散分布
可分为 Bernoulli 伯努利分布 (bernoulli distribution )和二项随机分布(binomial distribution)
注意: 伯努利分布是只做一次实验的二项随机分布,二项随机分布是多次的伯努利随机分布
伯努利的条件是1) 独立事件 2) 概率稳定

要如何求bernoulli random variable 的期望和方差呢?
求ernoulli random variable 的期望(expectation-均值)E(x)=1*p +0*(1-p)=p
求variance =方差就是点到均值的距离的平方的平值(有权重=概率)
故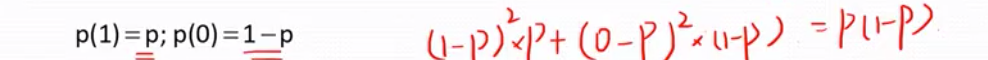
明白了伯努利随机变量的期望和方差就可以继续拓展,二项随机变量就是多次的伯努利事件,所以分别✖️n 次就是二项随机变量的期望和方差

互斥事件一定是有关系的,不可能 是独立事件


求方差本质上就是求期望,但是方差有一个缺点,就是会将单位也平方,所以求标准方差。

小结:
如果只有一个随机变量看均值和方差
如果有两个随机变量用协方差和相关性系数
计数原理:用于统计出现的次数

乘法规则
阶乘规则
标签规则



两组数据的关系,比如两个股票
两组数据的关系涉及到两个指标即(covariance- & correlation)

Covariance 协方差 这个指标主要是用来看2组数据是同向变化还是反向变化的

注意:因为是样本, 所以分母是n-1 如果是总体分母就是n


散点图最适合用来描述2组数据的关系
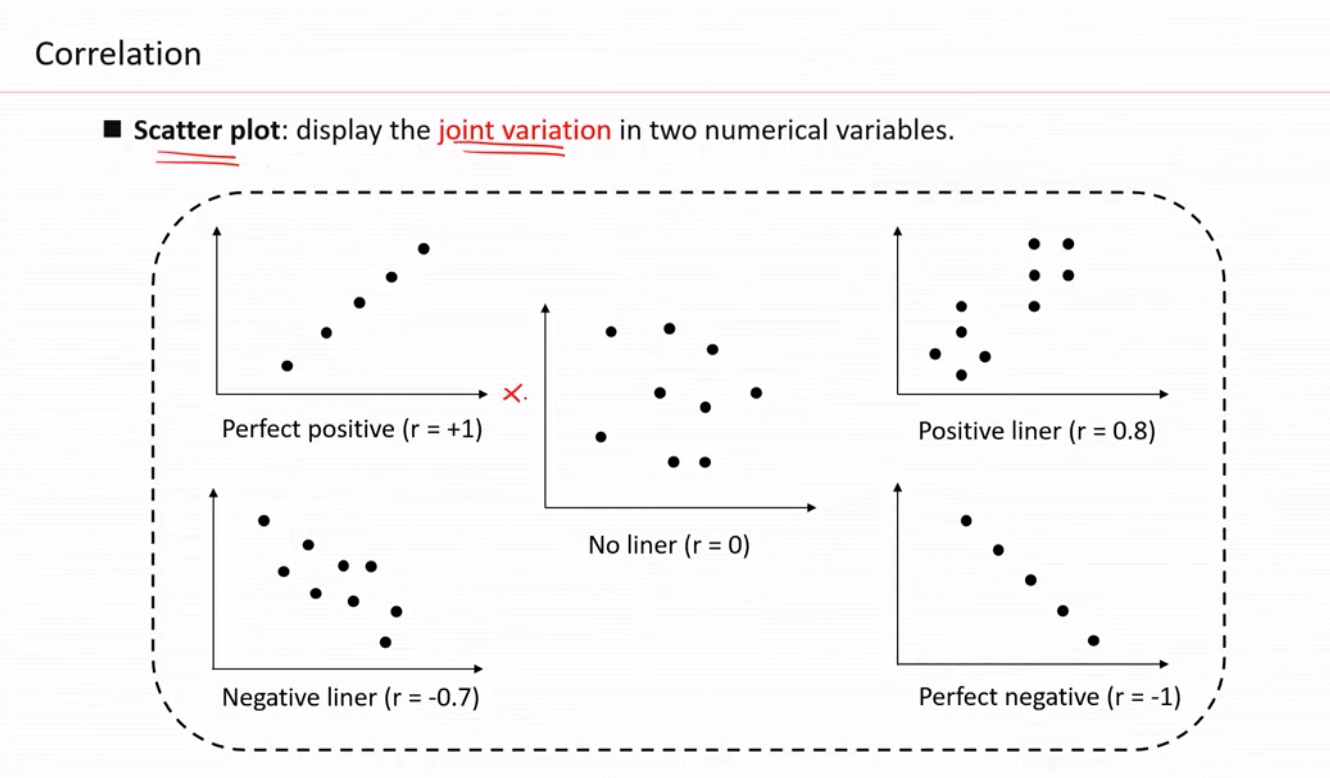
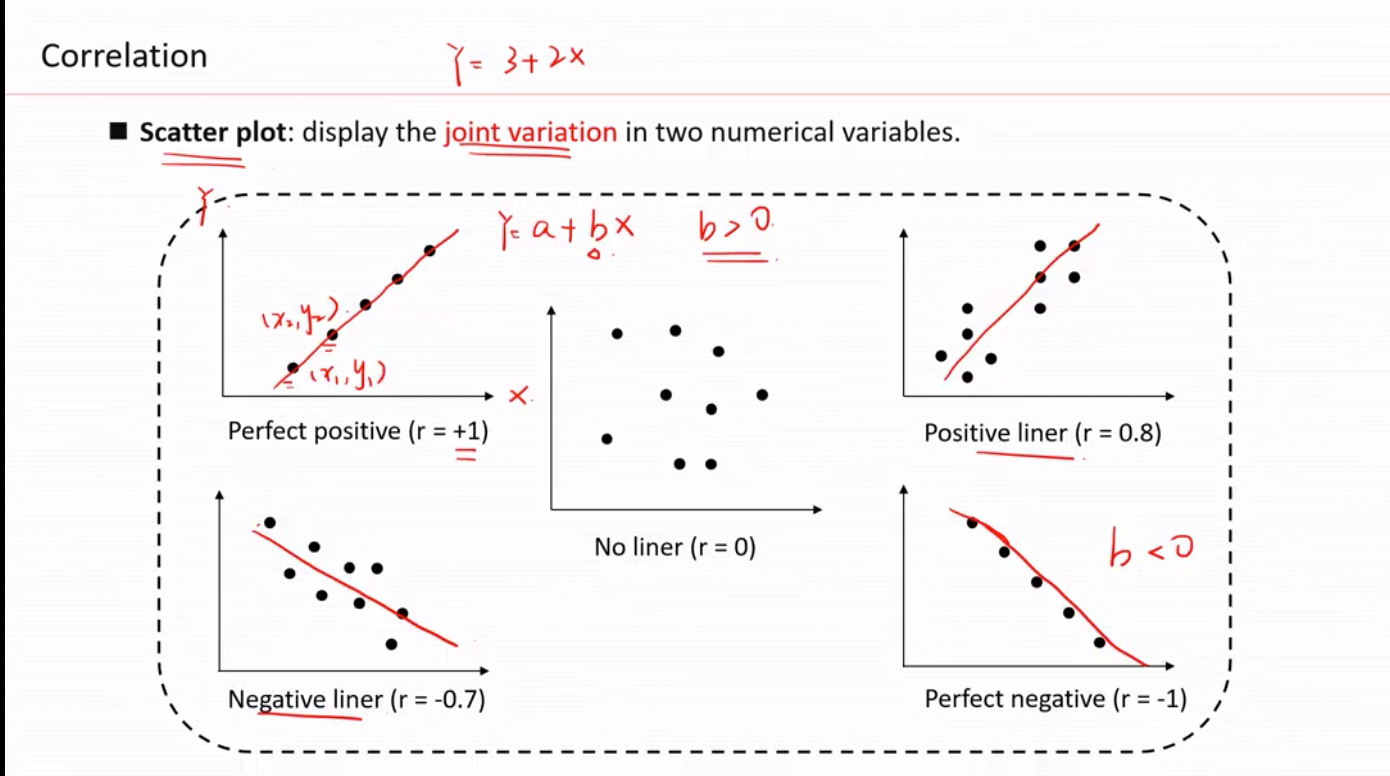
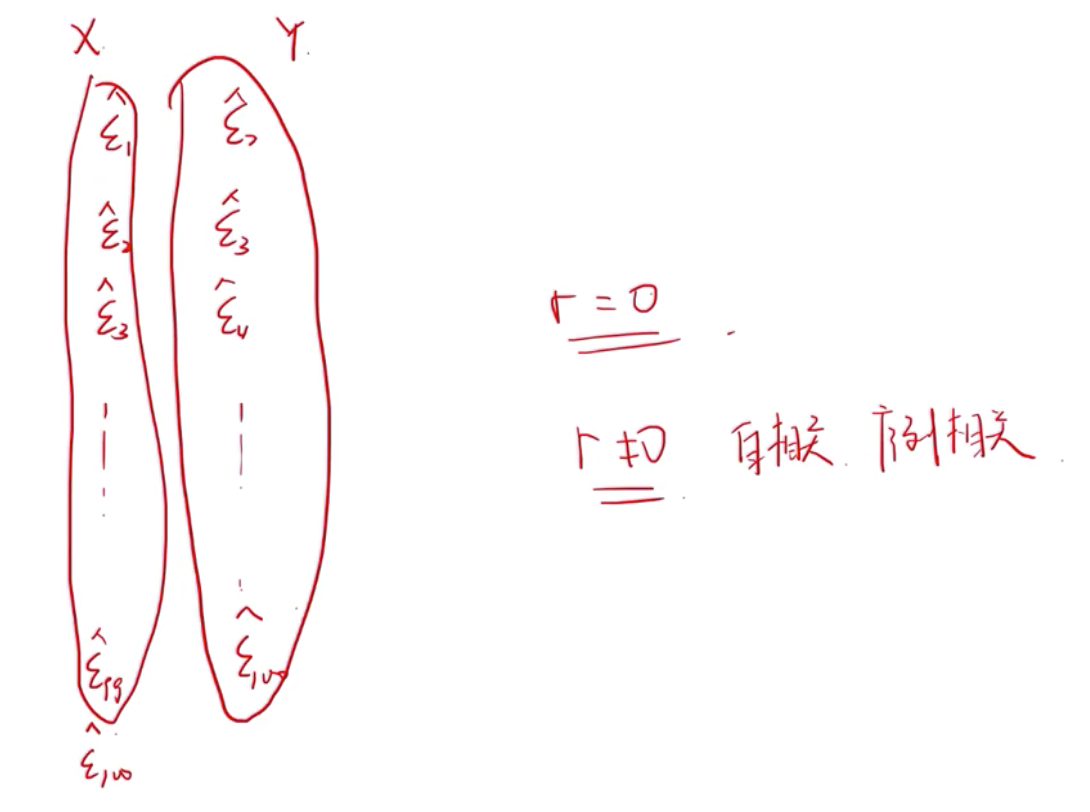
注意 correltion ratio != 斜率
左上图( r=1, 只能说明线性关系>0, 不代表这条线的斜率是1)
r=0 只代表没有线性关系,不代表没有关系。eg. y=x^2 , r=0